Data: Type and Distribution
Aly Lamuri
Indonesia Medical Education and Research Institute
Overview
- Data type
- Probability Density Function
- Goodness of fit test
- Test of normality
- Central Limit Theorem
Data Type
- Categorical
- Numeric
- Numerous conventions in describing data
- Understanding the nature behind categorical and numeric is more important
- Examples on established convention:
- Nominal, ordinal, interval, ratio
- Categorical, discrete, continuous
 Nominal
Nominal
Data Type
- Categorical
- Numeric
Other examples:
- Types of car
- Brands
- Netflix shows
 Ordinal
Ordinal
Data Type
- Categorical
- Numeric
Other examples:
- Disease severity
- Qualitative measure: bad → good
 Discrete (clue: countable)
Discrete (clue: countable)
Data Type
- Categorical
- Numeric
 Continuous (clue: measurable)
Continuous (clue: measurable)
Data Type
- Categorical
- Numeric
Continuous:
- Interval
- Ratio
Continuous Data
Interval
- Has a fixed distance
- Arithmetic: addition and subtraction
- Examples:
- Likert scale
- Temperature in other scales
Ratio
- Has an absolute zero
- Infinitesimal measure
- All arithmetic rules are applicable
- Examples:
- Temperature in Kelvin
- Weight
How about Likert-type item?
- Usually uses a distinctive scale out of 4, 5, 7 and 10 units
- Some regards Likert-type question as discrete counts
- While for others, a continuous interval
- Context-dependant
How about Likert-type item?
- Usually uses a distinctive scale out of 4, 5, 7 and 10 units
- Some regards Likert-type question as discrete counts
- While for others, a continuous interval
- Context-dependant
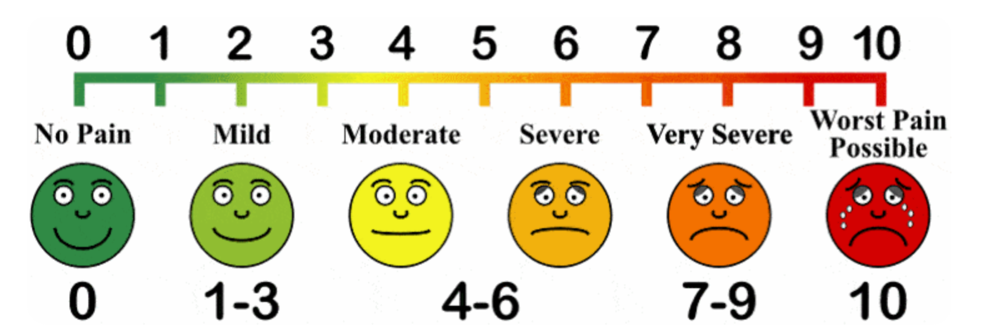
Checkpoint! What type of data do we have?
Checkpoint! What type of data do we have?
- We were conducting a survey in three universities.
Checkpoint! What type of data do we have?
- We were conducting a survey in three universities.
- From each university, we sampled the first, second, penultimate and final year students in a four-year programme.
Checkpoint! What type of data do we have?
- We were conducting a survey in three universities.
- From each university, we sampled the first, second, penultimate and final year students in a four-year programme.
- We nicely asked them to indicate their level of burnout using a Likert-type self-report inventory.
Checkpoint! What type of data do we have?
- We were conducting a survey in three universities.
- From each university, we sampled the first, second, penultimate and final year students in a four-year programme.
- We nicely asked them to indicate their level of burnout using a Likert-type self-report inventory.
- We also kindly measured their blood cortisol level.
Overview
- Data type
- Probability Density Function
- Goodness of fit test
- Test of normality
- Central Limit Theorem
Probability
- An event E occurring within a particular sample space S
- Event: Expected results
- Sample space: All possible outcomes
- Probability P is a proportion of event divided by its sample space
- Or mathematically:
P(E=e)=ES
- Suppose we have a fair coin and doing a flip 10 times, where
Hindicates the head andTindicates the tail
Probability
- An event E occurring within a particular sample space S
- Event: Expected results
- Sample space: All possible outcomes
- Probability P is a proportion of event divided by its sample space
- Or mathematically:
P(E=e)=ES
- Suppose we have a fair coin and doing a flip 10 times, where
Hindicates the head andTindicates the tail - Then, our sample space:
set.seed(1)S <- sample(c("H", "T"), 10, replace=TRUE, prob=rep(1/2, 2)) %T>% print()## [1] "T" "T" "H" "H" "T" "H" "H" "H" "H" "T"Probability
- An event E occurring within a particular sample space S
- Event: Expected results
- Sample space: All possible outcomes
- Probability P is a proportion of event divided by its sample space
- Or mathematically:
P(E=e)=ES
- Let the head be our expected outcome
Probability
- An event E occurring within a particular sample space S
- Event: Expected results
- Sample space: All possible outcomes
- Probability P is a proportion of event divided by its sample space
- Or mathematically:
P(E=e)=ES
- Let the head be our expected outcome
- Then, our event:
E <- S[which(S == "H")] %T>% print()## [1] "H" "H" "H" "H" "H" "H"Probability
- An event E occurring within a particular sample space S
- Event: Expected results
- Sample space: All possible outcomes
- Probability P is a proportion of event divided by its sample space
- Or mathematically:
P(E=e)=ES
- Thus, we can regard the probability of having a desired outcome as a relative frequency of events in a given sample space
Probability
- An event E occurring within a particular sample space S
- Event: Expected results
- Sample space: All possible outcomes
- Probability P is a proportion of event divided by its sample space
- Or mathematically:
P(E=e)=ES
- Thus, we can regard the probability of having a desired outcome as a relative frequency of events in a given sample space
- As such:
length(E) / length(S)## [1] 0.6Probability
- An event E occurring within a particular sample space S
- Event: Expected results
- Sample space: All possible outcomes
- Probability P is a proportion of event divided by its sample space
- Or mathematically:
P(E=e)=ES
- Thus, we can regard the probability of having a desired outcome as a relative frequency of events in a given sample space
- As such:
length(E) / length(S)## [1] 0.6- Ten flips using a fair coin resulted in 60% chance of having heads
## [1] "T" "T" "H" "H" "T" "H" "H" "H" "H" "T"Determine the Probability
- Enumeration
- Tree diagram
- Resampling
- So far, we have learnt about enumeration
- In such a method, we determine a probability as a relative frequency measure
Determine the Probability
- Enumeration
- Tree diagram
- Resampling
Caveats in enumeration
- Higher sample space → harder to solve
- It is more apparent with sequential problem
- Sequential problem: when you need to calculate probability from two different instances
- Example: the probability of having three
4while rolling a dice three times
- So far, we have learnt about enumeration
- In such a method, we determine a probability as a relative frequency measure
Determine the Probability
- Enumeration
- Tree diagram
- Resampling
Caveats in enumeration
- Higher sample space → harder to solve
- It is more apparent with sequential problem
- Sequential problem: when you need to calculate probability from two different instances
- Example: the probability of having three
4while rolling a dice three times
Tree diagram is available to solve a more complex probability problem
- So far, we have learnt about enumeration
- In such a method, we determine a probability as a relative frequency measure
Determine the Probability
- Enumeration
- Tree diagram
- Resampling
Sample case → the urn problem
- We have an urn filled with 30 blue and 50 red balls
- All balls are identical except for color
- In the urn, all balls have an equal distribution
- Task: Take three balls without replacement
- Question: How high is the chance of getting three blue balls?
Determine the Probability
- Enumeration
- Tree diagram
- Resampling
B (30/80) / /80 \ \ R (50/80)Determine the Probability
- Enumeration
- Tree diagram
- Resampling
B (29/79) / B (30/80) / \ / R (50/79)80 \ \ R (50/80)Determine the Probability
- Enumeration
- Tree diagram
- Resampling
/ B (28/78) B (29/79) / \ R (50/78) B (30/80) / \ / R (50/79)80 \ \ R (50/80)Determine the Probability
- Enumeration
- Tree diagram
- Resampling
/ B (28/78) B (29/79) / \ R (50/78) B (30/80) / \ / R (50/79)80 \ \ R (50/80)The chance for having three blue balls is 0.0494
Determine the Probability
- Enumeration
- Tree diagram
- Resampling
/ B (28/78) B (29/79) / \ R (50/78) B (30/80) / \ / B (?) / R (50/79)80 \ R (?) \ \ R (50/80)We have learnt how to draw a tree diagram. Now, what should we fill the question mark with?
Determine the Probability
- Enumeration
- Tree diagram
- Resampling
/ B (28/78) B (29/79) / \ R (50/78) B (30/80) / \ / B (29/78) / R (50/79)80 \ R (49/78) \ \ R (50/80)Let's roll the dice :)
- To learn resampling method, we will conduct a short experiment
- This experiment relies on a simple function
- Said function will simulate an independent dice-roll
- The only parameter is
n, indicating the number of roll
dice <- function(n) { sample(1:6, n, replace=TRUE, prob=rep(1/6, 6))}Let's roll the dice :)
- To learn resampling method, we will conduct a short experiment
- This experiment relies on a simple function
- Said function will simulate an independent dice-roll
- The only parameter is
n, indicating the number of roll
dice <- function(n) { sample(1:6, n, replace=TRUE, prob=rep(1/6, 6))}Let's see whether our function work...
Let's roll the dice :)
- To learn resampling method, we will conduct a short experiment
- This experiment relies on a simple function
- Said function will simulate an independent dice-roll
- The only parameter is
n, indicating the number of roll
dice <- function(n) { sample(1:6, n, replace=TRUE, prob=rep(1/6, 6))}Let's see whether our function work...
dice(1)## [1] 3It does!
Let's roll the dice :)
- So we shall roll the dice 10 times
- Let 4 be our outcome of interest
- How high is the probability of having the event within 10 trials?
Let's roll the dice :)
- So we shall roll the dice 10 times
- Let 4 be our outcome of interest
- How high is the probability of having the event within 10 trials?
set.seed(1)roll <- dice(10) %T>% print()## [1] 3 4 5 1 3 1 1 5 5 2- How high is the probability of getting 4?
Let's roll the dice :)
- So we shall roll the dice 10 times
- Let 4 be our outcome of interest
- How high is the probability of having the event within 10 trials?
set.seed(1)roll <- dice(10) %T>% print()## [1] 3 4 5 1 3 1 1 5 5 2- How high is the probability of getting 4?
- Turns out, it is 1/10
Let's roll the dice :)
- So we shall roll the dice 10 times
- Let 4 be our outcome of interest
- How high is the probability of having the event within 10 trials?
set.seed(1)roll <- dice(10) %T>% print()## [1] 3 4 5 1 3 1 1 5 5 2- How high is the probability of getting 4?
- Turns out, it is 1/10
- We have a fair dice, why is the probability not 1/6?
Let's roll the dice :)
- So we shall roll the dice 10 times
- Let 4 be our outcome of interest
- How high is the probability of having the event within 10 trials?
set.seed(1)roll <- dice(10) %T>% print()## [1] 3 4 5 1 3 1 1 5 5 2- How high is the probability of getting 4?
- Turns out, it is 1/10
- We have a fair dice, why is the probability not 1/6?
- Hint: sample and population
Let's roll the dice :)
- So we shall roll the dice 10 times
- Let 4 be our outcome of interest
- How high is the probability of having the event within 10 trials?
set.seed(1)roll <- dice(10) %T>% print()## [1] 3 4 5 1 3 1 1 5 5 2- How high is the probability of getting 4?
- Turns out, it is 1/10
- We have a fair dice, why is the probability not 1/6?
- Hint: sample and population
- The more sample we got, the closer it is to represent the population
Let's roll the dice :)
- What will we get with different number of rolls?
Let's roll the dice :)
- What will we get with different number of rolls?
- 100 rolls:
set.seed(1); roll <- dice(100)sum(roll==4) / length(roll)## [1] 0.25Let's roll the dice :)
- What will we get with different number of rolls?
- 100 rolls:
set.seed(1); roll <- dice(100)sum(roll==4) / length(roll)## [1] 0.25- 1,000 rolls:
set.seed(1); roll <- dice(1000)sum(roll==4) / length(roll)## [1] 0.2Let's roll the dice :)
- What will we get with different number of rolls?
- 100 rolls:
set.seed(1); roll <- dice(100)sum(roll==4) / length(roll)## [1] 0.25- 1,000 rolls:
set.seed(1); roll <- dice(1000)sum(roll==4) / length(roll)## [1] 0.2- 10,000 rolls:
set.seed(1); roll <- dice(10000)sum(roll==4) / length(roll)## [1] 0.1724Let's roll the dice :)
- 100,000 rolls:
set.seed(1); roll <- dice(100000)sum(roll==4) / length(roll)## [1] 0.1661Let's roll the dice :)
- 100,000 rolls:
set.seed(1); roll <- dice(100000)sum(roll==4) / length(roll)## [1] 0.1661- 1,000,000 rolls:
set.seed(1); roll <- dice(1000000)sum(roll==4) / length(roll)## [1] 0.1664Let's roll the dice :)
- 100,000 rolls:
set.seed(1); roll <- dice(100000)sum(roll==4) / length(roll)## [1] 0.1661- 1,000,000 rolls:
set.seed(1); roll <- dice(1000000)sum(roll==4) / length(roll)## [1] 0.1664- 10,000,000 rolls:
set.seed(1); roll <- dice(10000000)sum(roll==4) / length(roll)## [1] 0.1666Let's roll the dice :)
- With more trials, we get closer to the expected probability in a fair dice
- Which is 1/6, or equivalently 0.1667
- The error of estimated probability is inversely proportional to the number of trial
Let's roll the dice :)
- With more trials, we get closer to the expected probability in a fair dice
- Which is 1/6, or equivalently 0.1667
- The error of estimated probability is inversely proportional to the number of trial
Or mathematically:
ϵ=√^p(1−^p)N, where:
ϵ: Error
^p: Estimated probability (current trial)
N: Number of resampling
Let's roll the dice :)
How high is the error in our trials?
Let's roll the dice :)
How high is the error in our trials?
- First we need to set the function to calculate error
epsilon <- function(p.hat, n) { sqrt({p.hat * (1-p.hat)}/n)}Let's roll the dice :)
How high is the error in our trials?
- First we need to set the function to calculate error
epsilon <- function(p.hat, n) { sqrt({p.hat * (1-p.hat)}/n)}- Get the roll and probability
roll <- c(10, 100, 1000, 10000, 100000, 1000000, 10000000)prob <- sapply(roll, function(n) { set.seed(1); roll <- dice(n) sum(roll==4) / length(roll)})Let's roll the dice :)
df <- data.frame(list("roll"=roll, "prob"=prob))df %>% knitr::kable() %>% kable_styling()| roll | prob |
|---|---|
| 1e+01 | 0.1000 |
| 1e+02 | 0.2500 |
| 1e+03 | 0.2000 |
| 1e+04 | 0.1724 |
| 1e+05 | 0.1661 |
| 1e+06 | 0.1664 |
| 1e+07 | 0.1666 |
Let's roll the dice :)
df <- data.frame(list("roll"=roll, "prob"=prob))df %>% knitr::kable() %>% kable_styling()| roll | prob |
|---|---|
| 1e+01 | 0.1000 |
| 1e+02 | 0.2500 |
| 1e+03 | 0.2000 |
| 1e+04 | 0.1724 |
| 1e+05 | 0.1661 |
| 1e+06 | 0.1664 |
| 1e+07 | 0.1666 |
df$error <- mapply(function(p.hat, n) { epsilon(p.hat, n)}, p.hat=df$prob, n=df$roll) %T>% print()## [1] 0.0948683 0.0433013 0.0126491 0.0037773 0.0011769 0.0003724 0.0001178Let's roll the dice :)
Here is a nice figure to summarize the concept:

Let's roll the dice :)
And another figure to see the error:

Homework
- Previously, we used tree diagram to determine the probability in the urn problem
- Solve the urn problem using resampling method
- Question: What is the probability of getting three red balls?
Homework
- Previously, we used tree diagram to determine the probability in the urn problem
- Solve the urn problem using resampling method
- Question: What is the probability of getting three red balls?
Task description:
- Do a trial of {100,200,500,1000,2000,5000}
- Set
1as the seed for each resampling - Plot the probability and error
- Briefly explain your results
- You may use any programming language you are familiar with
- You just need to present the plot and explanation
Random Variables
Independent vs Identical? → I.I.D
Random Variables
Independent vs Identical? → I.I.D
- All sampled random variables should be independent from one another
- Each sampling procedure have to be identical, as to produce similar probability
Random Variables
Independent vs Identical? → I.I.D
- All sampled random variables should be independent from one another
- Each sampling procedure have to be identical, as to produce similar probability
Considering I.I.D, can we do a better probability estimation?
Random Variables
Independent vs Identical? → I.I.D
- All sampled random variables should be independent from one another
- Each sampling procedure have to be identical, as to produce similar probability
Considering I.I.D, can we do a better probability estimation?
- If they are I.I.D, we can approximate the probability using:
- Probability Mass Function (discrete variable)
- Probability Density Function (continuous variable)
Random Variables
Independent vs Identical? → I.I.D
- All sampled random variables should be independent from one another
- Each sampling procedure have to be identical, as to produce similar probability
Considering I.I.D, can we do a better probability estimation?
- If they are I.I.D, we can approximate the probability using:
- Probability Mass Function (discrete variable)
- Probability Density Function (continuous variable)
In math, please?
P(E=e)=f(e)>0:E∈S∑e∈Sf(e)=1P(E∈A)=∑e∈Af(e):A⊂S(1)(2)(3)
- The function is arbitrary, it can take on any form
- There are myriad distributions
- We will look at specific examples
Binomial Distribution
- Have an identical iteration over n times of trial
- Each iteration corresponds to a Bernoulli trial
- All instances are independent
Binomial Distribution
- Have an identical iteration over n times of trial
- Each iteration corresponds to a Bernoulli trial
- All instances are independent
f(x)=(nx)px(1−p)n−x(nx)=n!x!(n−x)!(1)
Or simply denoted as: X∼B(n,p)
Binomial Distribution
- Have an identical iteration over n times of trial
- Each iteration corresponds to a Bernoulli trial
- All instances are independent
f(x)=(nx)px(1−p)n−x(nx)=n!x!(n−x)!(1)
Or simply denoted as: X∼B(n,p)
μ=n⋅pσ=√μ⋅(1−p)
Binomial Distribution
- Have an identical iteration over n times of trial
- Each iteration corresponds to a Bernoulli trial
- All instances are independent

Binomial Distribution
- Have an identical iteration over n times of trial
- Each iteration corresponds to a Bernoulli trial
- All instances are independent

Geometric Distribution
- Describes number of failures before getting an event
- Follows Bernoulli trial
- A derivation of binomial distribution, with x=1
Geometric Distribution
- Describes number of failures before getting an event
- Follows Bernoulli trial
- A derivation of binomial distribution, with x=1
f(n)=P(X=n)=p(1−p)n−1,with:
n: Number of trials to get an event
p: The probability of getting an event
Or simply denoted as X∼G(p)
Geometric Distribution
- Describes number of failures before getting an event
- Follows Bernoulli trial
- A derivation of binomial distribution, with x=1
f(n)=P(X=n)=p(1−p)n−1,with:
n: Number of trials to get an event
p: The probability of getting an event
Or simply denoted as X∼G(p)
μ=1pσ=√1−pp2
Geometric Distribution
- Describes number of failures before getting an event
- Follows Bernoulli trial
- A derivation of binomial distribution, with x=1

Poisson Distribution
- Suppose we know the rate of certain outcomes
- Poisson distribution defines the probability of an outcome happening x times
- Limited to a particular time frame (often described as observation period)
Poisson Distribution
- Suppose we know the rate of certain outcomes
- Poisson distribution defines the probability of an outcome happening x times
- Limited to a particular time frame (often described as observation period)
f(x)=e−λλxx!, with:
x: The number of expected events
e: Euler's number
λ: Average number of events in one time frame
Or simply denoted as X∼P(λ)
μ=λσ=√λ
Poisson Distribution
- Suppose we know the rate of certain outcomes
- Poisson distribution defines the probability of an outcome happening x times
- Limited to a particular time frame (often described as observation period)

Uniform Distribution
- A continuous function describing uniform probabilities
- Hence the name: uniform distribution
- Useful in random number generator → for randomization in clinical trials
- We finished the first part of distribution: discrete
- Now, we shall see continuous distributions and their properties
Uniform Distribution
- A continuous function describing uniform probabilities
- Hence the name: uniform distribution
- Useful in random number generator → for randomization in clinical trials
f(x)=1b−a
Or simply denoted as X∼U(a,b)
- We finished the first part of distribution: discrete
- Now, we shall see continuous distributions and their properties
Uniform Distribution
- A continuous function describing uniform probabilities
- Hence the name: uniform distribution
- Useful in random number generator → for randomization in clinical trials
f(x)=1b−a
Or simply denoted as X∼U(a,b)
μ=b+a2σ=(b−a)212
- We finished the first part of distribution: discrete
- Now, we shall see continuous distributions and their properties
Uniform Distribution
- A continuous function describing uniform probabilities
- Hence the name: uniform distribution
- Useful in random number generator → for randomization in clinical trials

- We finished the first part of distribution: discrete
- Now, we shall see continuous distributions and their properties
Exponential Distribution
- A reparameterization of Poisson distribution
- We are interested to see how long of a time frame needed to observe an event
- Time frame is intangible
- It is not always time, it could be other continuous measures
- Examples: Mileage, weight, volume, etc.
Exponential Distribution
- A reparameterization of Poisson distribution
- We are interested to see how long of a time frame needed to observe an event
f(x)=λe−xλ,with:
x: Time needed to observe an event
λ: The rate for a certain event
Or simply denoted as X∼Exponential(λ)
μ=σ=1λ
- Time frame is intangible
- It is not always time, it could be other continuous measures
- Examples: Mileage, weight, volume, etc.
Exponential Distribution
- A reparameterization of Poisson distribution
- We are interested to see how long of a time frame needed to observe an event

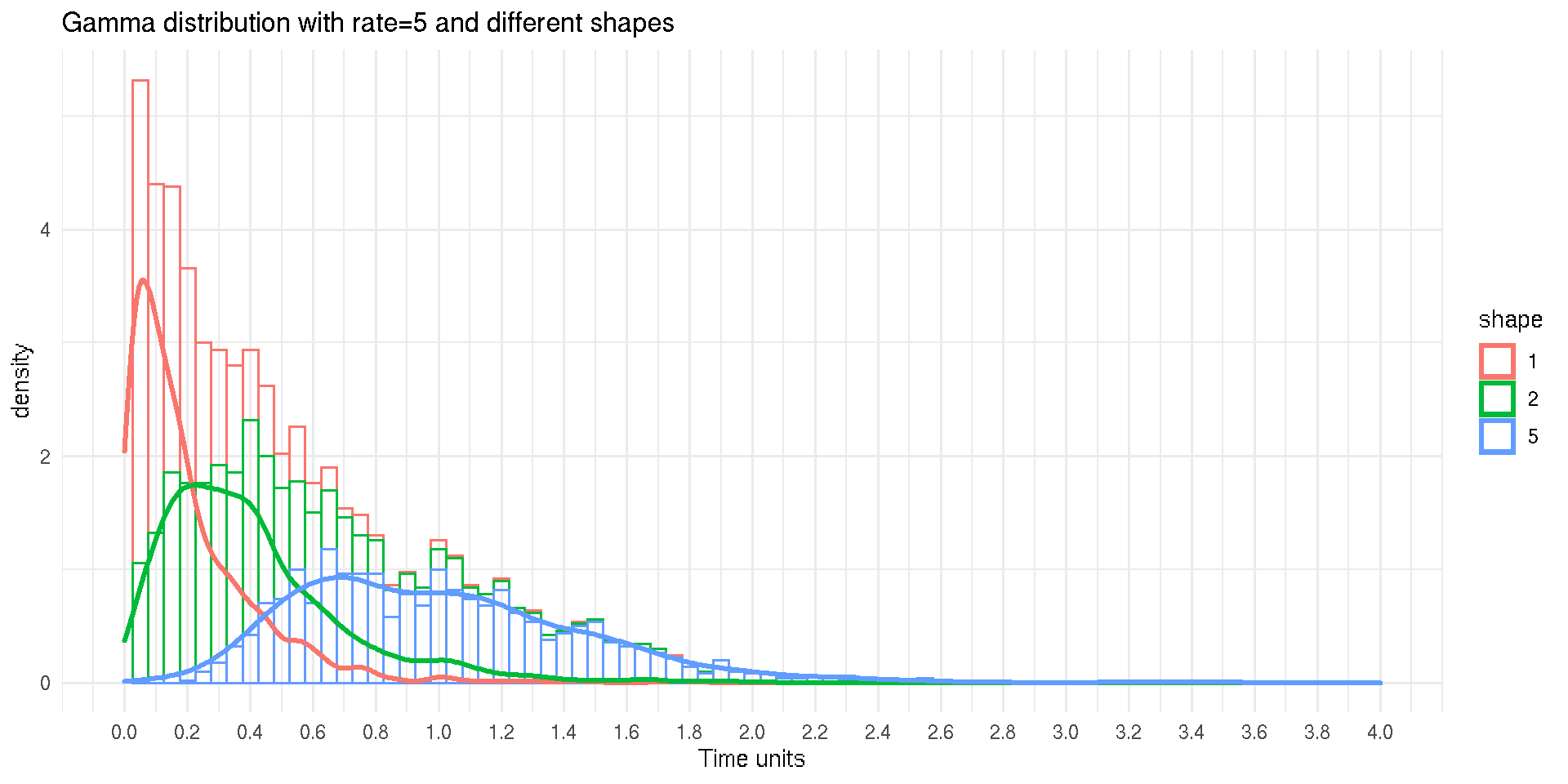
Gamma Distribution
- Exponential distribution is a gamma distribution without a shape parameter
- Essentially, gamma distribution finds its uses in similar cases as exponential distribution
- Relies on the gamma function Γ(α)
Gamma Distribution
- Exponential distribution is a gamma distribution without a shape parameter
- Essentially, gamma distribution finds its uses in similar cases as exponential distribution
- Relies on the gamma function Γ(α)
f(x)=βαΓ(α)xα−1e−xβΓ(α)=∫∞0yα−1e−y dy, with:
β: Rate ( λ in exponential PDF)
α: Shape
Γ: Gamma function
e: Euler number
Or simply denoted as X∼Γ(α,β)
Gamma Distribution
- Exponential distribution is a gamma distribution without a shape parameter
- Essentially, gamma distribution finds its uses in similar cases as exponential distribution
- Relies on the gamma function Γ(α)
f(x)=βαΓ(α)xα−1e−xβΓ(α)=∫∞0yα−1e−y dy, with:
β: Rate ( λ in exponential PDF)
α: Shape
Γ: Gamma function
e: Euler number
Or simply denoted as X∼Γ(α,β)
If we were to assign the shape parameter α=1, we get an exponential PDF.
Gamma Distribution
- Exponential distribution is a gamma distribution without a shape parameter
- Essentially, gamma distribution finds its uses in similar cases as exponential distribution
- Relies on the gamma function Γ(α)
f(x)=βαΓ(α)xα−1e−xβΓ(α)=∫∞0yα−1e−y dy, with:
β: Rate ( λ in exponential PDF)
α: Shape
Γ: Gamma function
e: Euler number
Or simply denoted as X∼Γ(α,β)
If we were to assign the shape parameter α=1, we get an exponential PDF. Therefore, Exponential(λ)∼Γ(1,λ).
Gamma Distribution
- Exponential distribution is a gamma distribution without a shape parameter
- Essentially, gamma distribution finds its uses in similar cases as exponential distribution
- Relies on the gamma function Γ(α)
f(x)=βαΓ(α)xα−1e−xβΓ(α)=∫∞0yα−1e−y dy, with:
β: Rate ( λ in exponential PDF)
α: Shape
Γ: Gamma function
e: Euler number
Or simply denoted as X∼Γ(α,β)
If we were to assign the shape parameter α=1, we get an exponential PDF. Therefore, Exponential(λ)∼Γ(1,λ).
μ=αβσ=√αβ
Gamma Distribution
- Exponential distribution is a gamma distribution without a shape parameter
- Essentially, gamma distribution finds its uses in similar cases as exponential distribution
- Relies on the gamma function Γ(α)
χ2 Distributions
- Special cases of a Gamma distribution
- Widely used in statistical inferences
χ2 Distributions
- Special cases of a Gamma distribution
- Widely used in statistical inferences
f(x)=1Γ(k/2)2k/2xk/2−1e−x/2, with:
k: Degree of freedom
The rest are Gamma PDF derivations
Or simply denoted as X∼χ2(k)
μ=kσ=√2k
χ2 Distributions
- Special cases of a Gamma distribution
- Widely used in statistical inferences
f(x)=1Γ(k/2)2k/2xk/2−1e−x/2, with:
k: Degree of freedom
The rest are Gamma PDF derivations
Or simply denoted as X∼χ2(k)
μ=kσ=√2k
Relation to normal distribution?
χ2 Distributions
- Special cases of a Gamma distribution
- Widely used in statistical inferences

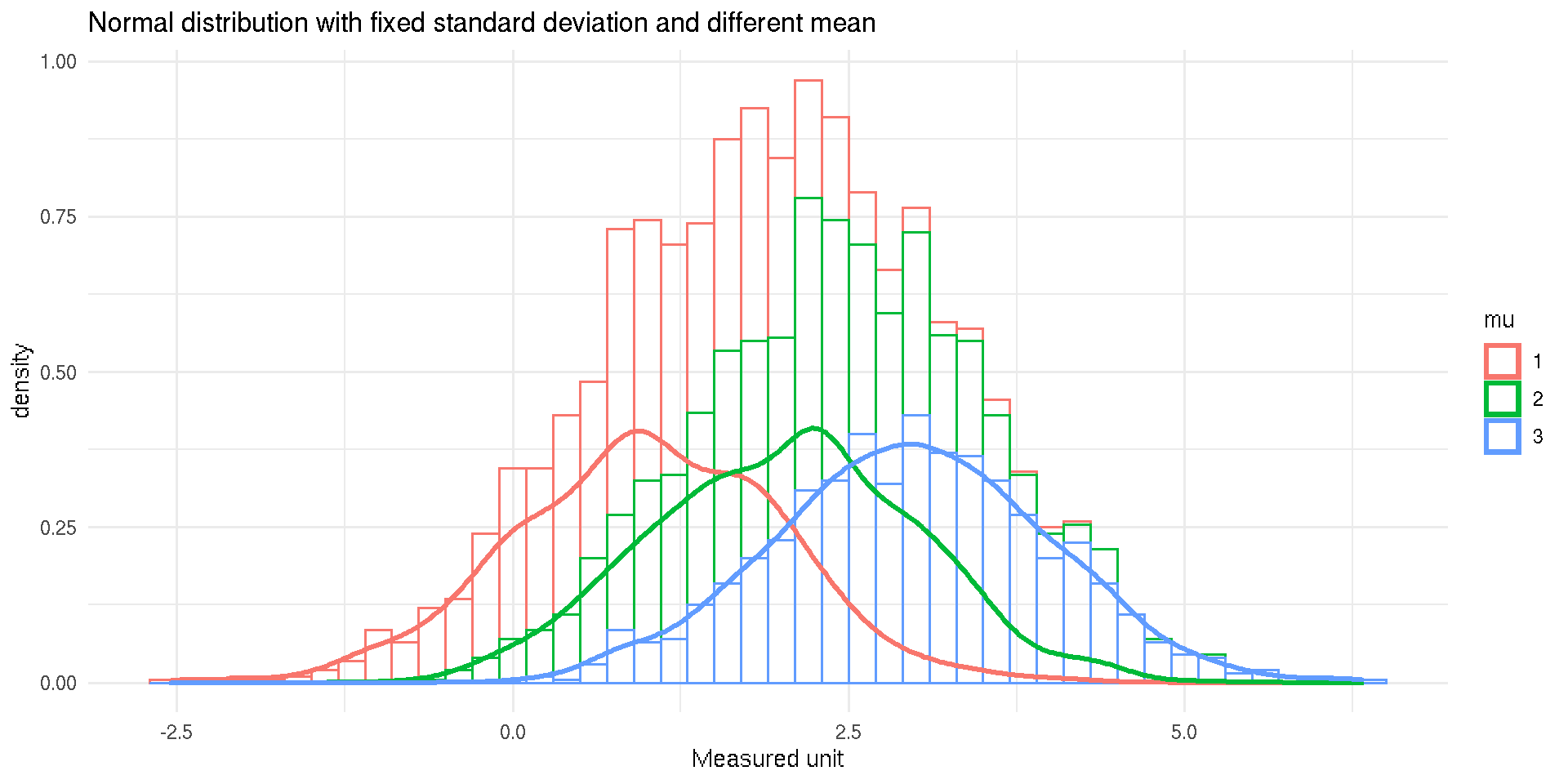
Normal Distribution
- Ubiquitous in real-world data
- Symmetric with μ and σ completely describes the distribution
Normal Distribution
- Ubiquitous in real-world data
- Symmetric with μ and σ completely describes the distribution
f(x)=1σ√2πexp{−12(x−μσ)2}, with:
x∈R:−∞<x<∞
μ∈R:−∞<μ<∞
σ∈R:0<σ<∞
Or simply denoted as X∼N(μ,σ)
Normal Distribution
- Ubiquitous in real-world data
- Symmetric with μ and σ completely describes the distribution
Normal Distribution
- Ubiquitous in real-world data
- Symmetric with μ and σ completely describes the distribution

Normal Distribution
- Ubiquitous in real-world data
- Symmetric with μ and σ completely describes the distribution

Overview
- Data type
- Probability Density Function
- Goodness of fit test
- Test of normality
- Central Limit Theorem
Goodness of Fit Test
- To determine whether your data follow a certain distribution
- Numerous methods exist, we will dig into more popular ones
- Given correct parameters, some methods can fully describe your data
- H0: Given data follow a certain distribution
- H1: Given data does not follow a certain distribution
Binomial Test
- An adaptation from binomial PMF
- To determine whether acquired probability followed Bernoulli trial's
Pr(X=k)=(nk)pk(1−p)n−k
Binomial Test
- An adaptation from binomial PMF
- To determine whether acquired probability followed Bernoulli trial's
Remember we previously tossed a coin 10 times?
Binomial Test
- An adaptation from binomial PMF
- To determine whether acquired probability followed Bernoulli trial's
Remember we previously tossed a coin 10 times?
set.seed(1)S <- sample(c("H", "T"), 10, replace=TRUE, prob=rep(1/2, 2)) %T>% print()## [1] "T" "T" "H" "H" "T" "H" "H" "H" "H" "T"length(E) / length(S)## [1] 0.6Binomial Test
- An adaptation from binomial PMF
- To determine whether acquired probability followed Bernoulli trial's
Remember we previously tossed a coin 10 times?
set.seed(1)S <- sample(c("H", "T"), 10, replace=TRUE, prob=rep(1/2, 2)) %T>% print()## [1] "T" "T" "H" "H" "T" "H" "H" "H" "H" "T"length(E) / length(S)## [1] 0.6If it represents a Bernoulli trial, it should satisfy P(X=6) in such a way that we cannot reject the H0 when calculating its probability:
P(X=6)=(106)0.56(1−0.5)4
Binomial Test
- An adaptation from binomial PMF
- To determine whether acquired probability followed Bernoulli trial's
Luckily, we do not need to compute it by hand
Binomial Test
- An adaptation from binomial PMF
- To determine whether acquired probability followed Bernoulli trial's
Luckily, we do not need to compute it by hand (yet)
binom.test(x=6, n=10, p=0.5)## ## Exact binomial test## ## data: 6 and 10## number of successes = 6, number of trials = 10, p-value = 0.8## alternative hypothesis: true probability of success is not equal to 0.5## 95 percent confidence interval:## 0.2624 0.8784## sample estimates:## probability of success ## 0.6Binomial Test
- An adaptation from binomial PMF
- To determine whether acquired probability followed Bernoulli trial's
Luckily, we do not need to compute it by hand (yet)
binom.test(x=6, n=10, p=0.5)## ## Exact binomial test## ## data: 6 and 10## number of successes = 6, number of trials = 10, p-value = 0.8## alternative hypothesis: true probability of success is not equal to 0.5## 95 percent confidence interval:## 0.2624 0.8784## sample estimates:## probability of success ## 0.6Interpreting the p-value, we cannot reject the H0, so our coin toss followed the Bernoulli trial after all.
Kolmogorov-Smirnov Test
- This test is available to determine various distribution
- Works as a non-parametric test
- Pretty much robust, only second to Anderson-Darling test on normal distribution
Robustness based on yielded power
Kolmogorov-Smirnov Test
- This test is available to determine various distribution
- Works as a non-parametric test
- Pretty much robust, only second to Anderson-Darling test on normal distribution
Let X∼Exponential(2):n=100
set.seed(1); X <- rexp(n=100, rate=2)Robustness based on yielded power
Kolmogorov-Smirnov Test
- This test is available to determine various distribution
- Works as a non-parametric test
- Pretty much robust, only second to Anderson-Darling test on normal distribution
Let X∼Exponential(2):n=100
set.seed(1); X <- rexp(n=100, rate=2)By imputing λ variable, Kolmogorov-Smirnov can compute its goodness of fit
ks.result <- ks.test(X, pexp, rate=2)Robustness based on yielded power
Kolmogorov-Smirnov Test
- This test is available to determine various distribution
- Works as a non-parametric test
- Pretty much robust, only second to Anderson-Darling test on normal distribution
print(ks.result)## ## One-sample Kolmogorov-Smirnov test## ## data: X## D = 0.084, p-value = 0.5## alternative hypothesis: two-sidedRobustness based on yielded power
Visual Examination
- Okay, doing math is cool and all
- But in a large sample, even a small deviation will result in H0 rejection
- Which mean, previously mentioned tests are of no use!
- We can rely on some visual cues to determine the distribution though
Visual Examination
- Okay, doing math is cool and all
- But in a large sample, even a small deviation will result in H0 rejection
- Which mean, previously mentioned tests are of no use!
- We can rely on some visual cues to determine the distribution though
For this demonstration, I will again use the previous object X
Visual Examination

Visual Examination

Hey, that's a good start!
Visual Examination

Hey, that's a good start! This does not clearly suggest a specific distribution though :(
Visual Examination
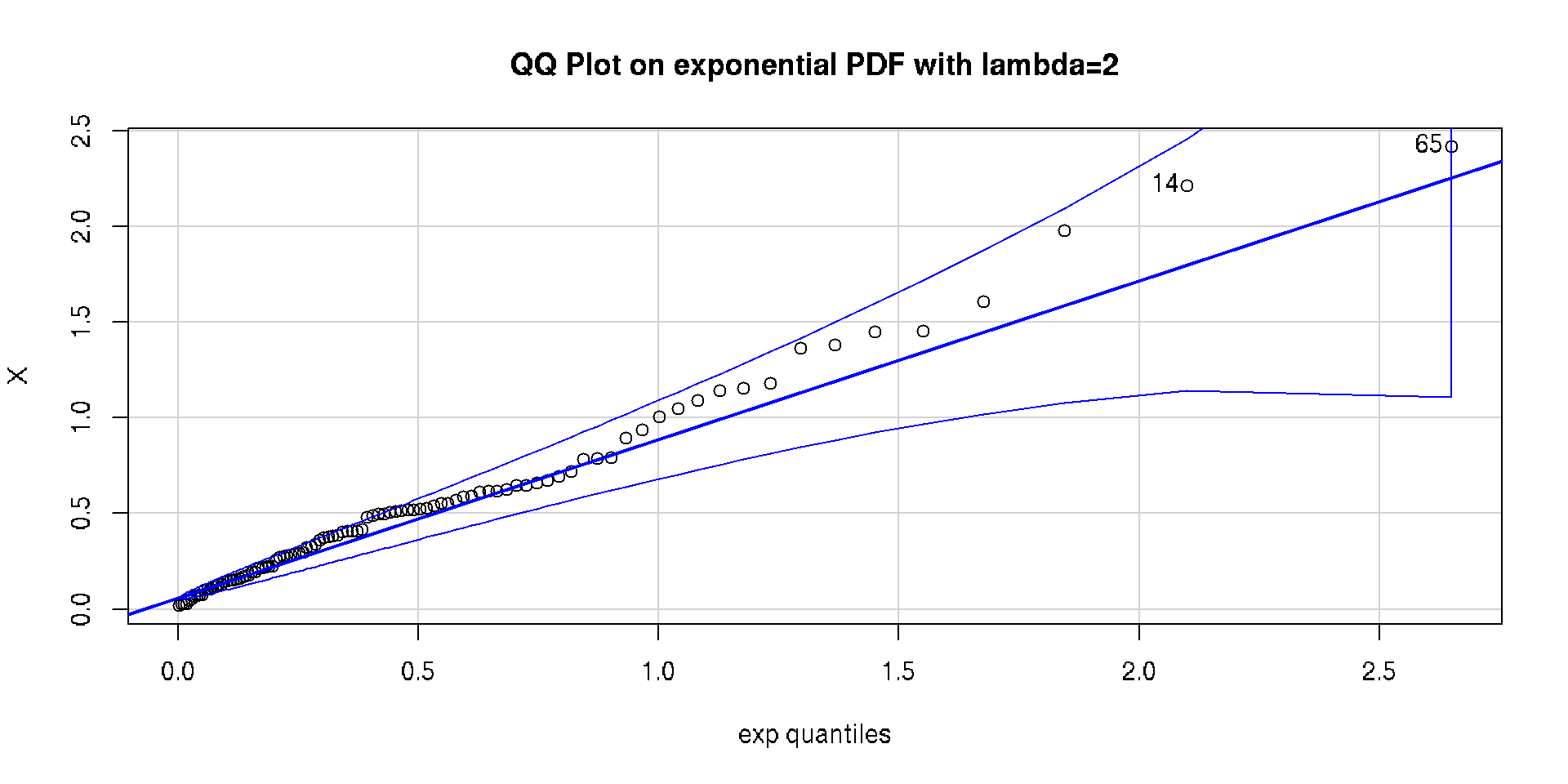
Visual Examination

Quantile-Quantile Plot (QQ Plot) can give a better visual cue :)
Overview
- Data type
- Probability Density Function
- Goodness of fit test
- Test of normality
- Central Limit Theorem
Test of Normality
- Practically a subset of goodness of fit test
- Some are more appropriate under certain circumstances
- We shall see through widely used ones
- H0: Sample follows the normal distribution
- H0: Sample does not follow the normal distribution
Shapiro-Wilk Test
- A well-established test to assess normality
- Can tolerate skewness to a certain degree
- Implementation in
R: sample size between 3 and 5000
Anderson-Darling Test
- Less well-known compared to Shapiro-Wilk
- Gives more weight to the tails
- Implementation in
R: minimum sample size is 7
Demonstration
Let X∼N(0,1):n=100
set.seed(1)X <- rnorm(n=100, mean=0, sd=1)Demonstration
Let X∼N(0,1):n=100
set.seed(1)X <- rnorm(n=100, mean=0, sd=1)Shapiro-Wilk
shapiro.test(X)## ## Shapiro-Wilk normality test## ## data: X## W = 1, p-value = 1Demonstration
Let X∼N(0,1):n=100
set.seed(1)X <- rnorm(n=100, mean=0, sd=1)Anderson-Darling
nortest::ad.test(X)## ## Anderson-Darling normality test## ## data: X## A = 0.16, p-value = 0.9Visual Examination

χ2 and Normal Distribution
- Raise a normally distributed data to the power of two
- It shall follow a χ2 distribution with 1 degree of freedom
χ2 and Normal Distribution
- Raise a normally distributed data to the power of two
- It shall follow a χ2 distribution with 1 degree of freedom
For demonstration purposes, we will re-use X∼N(0,1):n=100
set.seed(1)X <- rnorm(n=100, mean=0, sd=1)We previously tested X against Shapiro-Wilk and Anderson-Darling tests to indicate normality.
χ2 and Normal Distribution
- Raise a normally distributed data to the power of two
- It shall follow a χ2 distribution with 1 degree of freedom
For demonstration purposes, we will re-use X∼N(0,1):n=100
set.seed(1)X <- rnorm(n=100, mean=0, sd=1)We previously tested X against Shapiro-Wilk and Anderson-Darling tests to indicate normality.
Now, we will raise it to the power of two
X2 <- X^2χ2 and Normal Distribution
- Raise a normally distributed data to the power of two
- It shall follow a χ2 distribution with 1 degree of freedom
Does it still follow a normal distribution?
shapiro.test(X2)## ## Shapiro-Wilk normality test## ## data: X2## W = 0.7, p-value = 5e-13Visual Examination

χ2 and Normal Distribution
- Raise a normally distributed data to the power of two
- It shall follow a χ2 distribution with 1 degree of freedom
It does not follow normal distribution at all.
χ2 and Normal Distribution
- Raise a normally distributed data to the power of two
- It shall follow a χ2 distribution with 1 degree of freedom
It does not follow normal distribution at all. Does it follow the χ2 distribution though?
χ2 and Normal Distribution
- Raise a normally distributed data to the power of two
- It shall follow a χ2 distribution with 1 degree of freedom
It does not follow normal distribution at all. Does it follow the χ2 distribution though?
ks.test(X2, pchisq, df=1)## ## One-sample Kolmogorov-Smirnov test## ## data: X2## D = 0.1, p-value = 0.2## alternative hypothesis: two-sidedVisual Examination

Overview
- Data type
- Probability Density Function
- Goodness of fit test
- Test of normality
- Central Limit Theorem
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
d→ is a convergence of random variables
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
- So far, we have learnt sampling distributions
- We are also able to compute the mean and standard deviation based on their parameters
- It just happened that the sample mean follow a normal distribution
- Central limit theorem delineates such an occurrence
- This rule applies to both discrete and continuous distribution
d→ is a convergence of random variables
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
- It comes with a trade though
- CLT requires n as a sufficiently large number
- The number of n depends on data skewness
- More skewed? More n required.
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
- Choose any distribution
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
- Choose any distribution
- Generate n random numbers using specified parameters
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
- Choose any distribution
- Generate n random numbers using specified parameters
- Compute the mean and variance based on previous parameters → Use it to generate a normal distribution
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
- Choose any distribution
- Generate n random numbers using specified parameters
- Compute the mean and variance based on previous parameters → Use it to generate a normal distribution
- Reuse the parameters to re-iterate step 2
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
- Choose any distribution
- Generate n random numbers using specified parameters
- Compute the mean and variance based on previous parameters → Use it to generate a normal distribution
- Reuse the parameters to re-iterate step 2
- Conduct the simulation for an arbitrary number of times (e.g. for convenience, 1000)
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
- Choose any distribution
- Generate n random numbers using specified parameters
- Compute the mean and variance based on previous parameters → Use it to generate a normal distribution
- Reuse the parameters to re-iterate step 2
- Conduct the simulation for an arbitrary number of times (e.g. for convenience, 1000)
- Calculate mean from all generated data → Make a histogram and compare it with step 3
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
How do we determine n?→ Simulation
- Choose any distribution
- Generate n random numbers using specified parameters
- Compute the mean and variance based on previous parameters → Use it to generate a normal distribution
- Reuse the parameters to re-iterate step 2
- Conduct the simulation for an arbitrary number of times (e.g. for convenience, 1000)
- Calculate mean from all generated data → Make a histogram and compare it with step 3
- Does not fit normal distribution? → Increase n
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
Why should you care?
- In a research settings, you may find differing average values
- It could happen despite following the exact procedure
- And it is frustrating!
- Knowing CLT, you can prove the difference is indeed within expectation
- Besides, the equation above looks cool ;)
Central Limit Theorem
¯Xd→N(μ,σ√n)as n→∞
Final Excerpts:
- CLT describes a tendency of a mean ¯x to follow normal distribution
- Requires a sufficient number of sample n
- A simple simulation can prove the theorem